Exercice : Exercice Mesure d'un méridien terrestre par triangulation
[EF] joue ici le rôle de la méridienne Dunkerque-Barcelone.
Le but est d'en mesurer la longueur.
Notre triangulation ne comporte que 4 triangles.
On décompose EF en EI + IJ + JK + KF.
Les résultats numériques seront donnés à 0,01 près.
Question
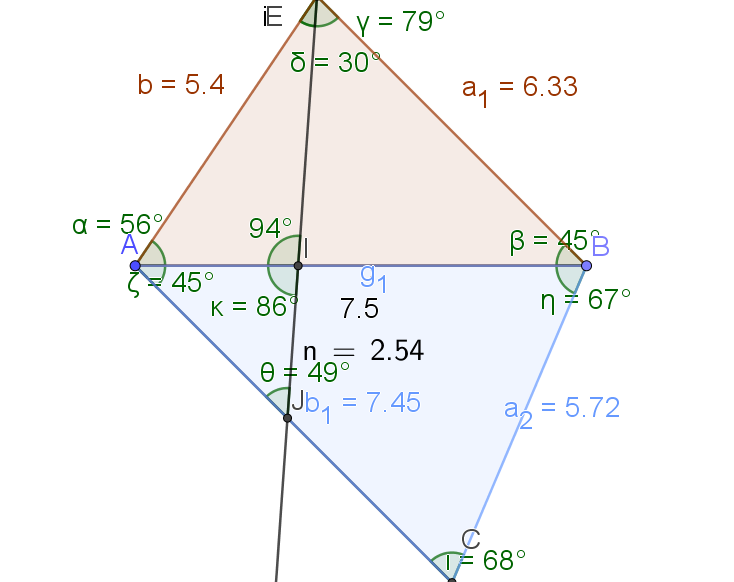
1. Les premières mesurent réalisées sont AB = 7,5 (la base), et les trois angles
\(\widehat{BAE} = 56°\)\(;\widehat{ABE} = 45°\) et \(\widehat{AEF} = 30°\).
a) Dans le triangle ABE, on connaît un côté et deux angles.
Calculer \(\widehat{AEB}\) puis avec la formule des sinus déterminer AE et EB.
Solution
\(\widehat{BAE} + \widehat{ABE}+\widehat{AEB}=180\)
\(56 + 45+\widehat{AEB}=180\)
\(101 +\widehat{AEB}=180\)
\(\widehat{AEB}=180-101=79°\)
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{B}}{b}=\frac{sin \widehat{E}}{e}\)
\(\frac{sin 56}{EB}=\frac{sin 45}{AE}=\frac{sin 79}{7,5}\)
\(\frac{sin 56}{EB}=\frac{sin 79}{7,5}\)
\(\frac{EB}{sin 56}=\frac{7,5}{sin 79}\)
\(EB=\frac{7,5}{sin 79}\times sin 56\)
\(EB\simeq6,33\)
\(\frac{sin 45}{AE}=\frac{sin 79}{7,5}\)
\(\frac{AE}{sin 45}=\frac{7,5}{sin 79}\)
\(AE=\frac{7,5}{sin 79}\times sin 45\)
\(AE=\frac{7,5}{sin 79}\times sin 45\)
\(AE\simeq5,4\)
Question
b) A présent, dans le triangle AEI on connaît un côté et deux angles. Déterminer \(\widehat{EIA}\) , EI et AI.
\(\color{red}{\textbf{EI est le premier morceau de notre méridienne.}}\)
Solution
\(\widehat{EIA}\)+\(\widehat{EAI}+\)\(\widehat{AEI}\)=180
\(\widehat{EIA}\)+56+30=180
\(\widehat{EIA}\)+86=180
\(\widehat{EIA}\)=180-86=94
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{I}}{i}=\frac{sin \widehat{E}}{e}\)
\(\frac{sin 56}{EI}=\frac{sin 94}{AE}=\frac{sin 30}{AI}\)
\(\frac{sin 56}{EI}=\frac{sin 94}{5,4}=\frac{sin 30}{AI}\)
\(\frac{sin 56}{EI}=\frac{sin 94}{5,4}\)
\(\frac{EI}{sin 56}=\frac{5,4}{sin 94}\)
\(EI=\frac{5,4}{sin 94}\times sin 56\)
\(EI\simeq4,49\)
\(\frac{sin 30}{AI}=\frac{sin 94}{5,4}\)
\(\frac{AI}{sin 30}=\frac{5,4}{sin 94}\)
\(AI=\frac{5,4}{sin 94}\times sin 30\)
\(AI\simeq2,71\)
Question
2. On mesure alors \(\widehat{BAC} = 45°\) et \(\widehat{ABC} = 67°.\)
a) Déterminer \(\widehat{ACB}\) puis AC.
Solution
\(\widehat{BAC}\)+\(\widehat{ABC}+\)\(\widehat{ACB}\)=180
45+67\(+\)\(\widehat{ACB}\)=180
112+\(+\)\(\widehat{ACB}\)=180
\(\widehat{ACB}\)=180-112=68°
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{B}}{b}=\frac{sin \widehat{C}}{c}\)
\(\frac{sin 45}{BC}=\frac{sin 67}{AC}=\frac{sin 68}{7,5}\)
\(\frac{sin 45}{BC}=\frac{sin 68}{7,5}\)
\(\frac{BC}{sin 45}=\frac{7,5}{sin 68}\)
\(BC=\frac{7,5}{sin 68} \times sin 45\)
\(BC\simeq 5,72\)
\(\frac{sin 67}{AC}=\frac{sin 68}{7,5}\)
\(\frac{AC}{sin 67}=\frac{7,5}{sin 68}\)
\(AC=\frac{7,5}{sin 68} \times sin 67\)
\(AC\simeq7,45\)
Question
b) Calculer \(\widehat{AIJ}\) ( on connaît \(\widehat{EIA}\) ).
Solution
\(\widehat{AIJ}+\widehat{EIA}\)=180°
\(\widehat{AIJ}+94=\)180°
\(\widehat{AIJ}=\)180-94
\(\widehat{AIJ}=\)86
Question
c) La résolution de AIJ est donc possible (on connaît AI). Déterminer IJ et AJ.
Solution
\(\frac{sin \widehat{A}}{a}=\frac{sin \widehat{I}}{i}=\frac{sin \widehat{J}}{j}\)
\(\frac{sin 45}{IJ}=\frac{sin 86}{AJ}=\frac{sin 49}{2,71}\)
\(\frac{sin 45}{IJ}=\frac{sin 49}{2,71}\)
\(\frac{IJ}{sin 45}=\frac{2,71}{sin 49}\)
\(IJ=\frac{2,71}{sin 49}\times sin 45\)
\(IJ=\frac{2,71}{sin 49}\times sin 45\)
\(IJ=\frac{2,71}{sin 49}\times sin 45\)
\(IJ\simeq2,54\)
\(\frac{sin 86}{AJ}=\frac{sin 49}{2,71}\)
\(\frac{AJ}{sin 86}=\frac{2,71}{sin 49}\)
\(AJ=\frac{2,71}{sin 49} \times sin 86\)
\(AJ=\frac{2,71}{sin 49} \times sin 86\simeq3,58\)
\(\color{magenta}{\textbf{Ainsi de proche en proche pour déterminer la longueur de toute la longueur EF}}\)
Quelques chiffres : La triangulation entre Dunkerque et Bacelone comporte 90 triangle ; durant cette aventure 500 000 mesures d'angles ont été effectuées ; l'estimation faite en 1980 (mesures effectuées par satellites) de la distance Dunkerque-Barcelone diffère de la valeur de Delambre et Méchain de ..... 10 mètres soit moins de 0,001%