Exercice : Exercice 36 :
Question
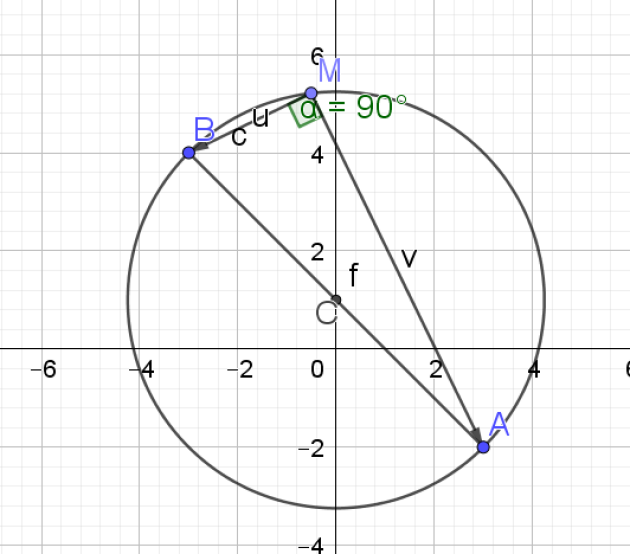
1.Donner l'équation du cercle \(C\) de diamètre [AB] où A(3 ; -2) et B(-3 ; 4)
Solution
Soit I le milieu du segment [AB] :
\(\begin{cases}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{3+(-3)}{2}\\y_I=\frac{-2+4}{2}\end{cases}\)
\(\iff \begin{cases}x_I=\frac{0}{2}\\y_I=\frac{2}{2}\end{cases}\)
\(\iff \begin{cases}x_I=0\\y_I=1\end{cases}\)
\(MI=\frac{AB}{2}\)
\(\iff MI^2=(\frac{AB}{2})^2\)
\(\iff MI^2=\frac{AB^2}{4}\)
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
\(\iff AB=\sqrt{(-3-3)^2+(4-(-2))^2}\)
\(\iff AB=\sqrt{(-6)^2+(6)^2}\)
\(\iff AB=\sqrt{36+36}\)
\(\iff AB=\sqrt{36 \times 2}\)
\(\iff AB=6\sqrt{2}\)
\(MI=\sqrt{(x_M-x_I)^2+(y_M-y_I)^2}\)
\(\iff MI=\sqrt{(x_M-0)^2+(y_M-1)^2}\)
\(\iff MI=\sqrt{x_M^2+(y_M-1)^2}\)
\(MI^2=\frac{AB^2}{4}\)
\(\iff x_M^2+(y_M-1)^2=\frac{(6\sqrt{2})^2}{4}\)
\(\iff x_M^2+(y_M-1)^2=\frac{36 \times 2}{4}\)
\(\iff x_M^2+(y_M-1)^2=\frac{72}{4}\)
\(\iff x_M^2+(y_M-1)^2=18\)
L'équation du cercle de diamètre [AB] est donc \(x_M^2+(y_M-1)^2=18\)
Question
2. Soit \(M (x ; y)\) un point du cercle \(C\). Que peut-on dire du produit scalaire \(\vec{MA}\).\(\vec{MB}\) ?
Question
3. En déduire qu'une équation du cercle C est : \(x^2 +y^2 - 2y-17 = 0.\)
Solution
\(\vec{MA}=\left( \begin{array}{c}3-x \\-2-y\end{array} \right)\)
\(\Longleftrightarrow\)\(\vec{MB}=\left( \begin{array}{c}-3-x \\4-y\end{array} \right)\)
\(\Longleftrightarrow\)\(\vec{MA}\).\(\vec{MB}\) =\(\left( \begin{array}{c}3-x \\-2-y\end{array} \right)\).\(\left( \begin{array}{c}-3-x \\4-y\end{array} \right)=0\)
\(\Longleftrightarrow\)\(\vec{MA}.\vec{MB} =(3-x)(-3-x)+(-2-y)(4-y)=0\)
\(\Longleftrightarrow\)\(\vec{MA}.\vec{MB} =3 \times (-3) +3 \times (-x) +(-x) \times (-3) +( -x) \times (-x)+(-2)\times 4 +(-2) \times (-y)+ (-y) \times 4 +(-y) \times (-y)=0\)
\(\Longleftrightarrow\)\(\vec{MA}.\vec{MB} =-9 -3x+ 3x +x^2+(-8)+2y -4y +y^2=0\)
\(\Longleftrightarrow\) \(x^2 +y^2 - 2y-17 = 0\)
Question
4. Déduire l'équation réduite du cercle C.
Solution
\(\color{magenta}\textbf{Déterminons l'équation réduite du cercle :}\)
Le centre du cercle est donc le point C milieu du segment [AB] :
\(x_C=\frac{x_A+x_B}{2}=\frac{3+(-3)}{2}=0\) \(\quad\) A(3 ; -2) et B(-3 ; 4)
\(y_C=\frac{y_A+y_B}{2}=\frac{-2+4}{2}=\frac{2}{2}=1\)
Le diamètre du cercle est la longueur du segment [AB] :
AB=\(\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-3-3)^2+(4-(-2))^2}=\sqrt{(-6)^2+(4+2)^2}=\sqrt{36+36}=\sqrt{2 \times 36}=6\sqrt{2}\)
Le rayon du cercle est la moitié de la longueur du segment [CD] :
\(\frac{AB}{2}\)=\(\frac{6\sqrt{2}}{2}=3\sqrt{2}\)
\(CM^2=R^2\)
\((x-x_C)^2+(y-y_C)^2=(3\sqrt{2})^2\)
\((x-0)^2+(y-1)^2=9 \times 2=18\)
\(\color{red}{x^2+(y-1)^2=18}\)