Exercice : Exercice 3ème ligne de niveau
On considère le plan muni d'un repère (O ;I ;J)
les points A et B ont pour coordonnées respectives
(2 ;-3) et (-1 ;1)
On note I le milieu du segment [AB].
M représente un point quelconque du plan et ses coordonnées
sont notées \((x ;y)\)
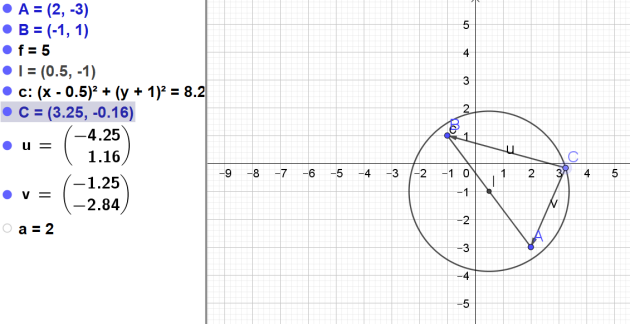
On s'intéresse au lieu géométrique E défini par la relation
\(\vec{MA}.\vec{MB}=2\)
Question
1.
a.Déterminer une relation entre \(x\) et \(y\) caractérisant l'ensemble E.
Solution
Calcul des coordonnées du point I milieu de [AB]
\(\iff \left( \begin{array}{c}2-x\\-3-y\end{array} \right). \left( \begin{array}{c}-1-x\\1-y\end{array}\right)=2\)
\(\iff (2-x)(-1-x)+(-3-y)(1-y)=2\)
\(\iff -2-2x+x+x^2-3+3y-y+y^2=2\)
\(\iff x^2-x+y^2+2y=2+5\)
\(\iff (x-\frac{1}{2})^2-\frac{1}{4}+(y+1)^2-1=2+5\)
\(\iff (x-\frac{1}{2})^2+(y+1)^2=2+5+\frac{1}{4}+1\)
\(\iff (x-\frac{1}{2})^2+(y+1)^2=8+\frac{1}{4}\)
\(\iff (x-\frac{1}{2})^2+(y+1)^2=\frac{32}{4}+\frac{1}{4}\)
\(\iff (x-\frac{1}{2})^2+(y+1)^2=\frac{33}{4}\)
\(\iff (x-\frac{1}{2})^2+(y+1)^2=\frac{33}{4}\)
Question
b.Vérifier que le point de coordonnées \((2 ;\sqrt{6}-1)\) appartient à l'ensemble E
Solution
b.\( (2-\frac{1}{2})^2+(\sqrt{6}-1+1)^2\)
\(=(\frac{4}{2}-\frac{1}{2})^2+(\sqrt{6})^2\)
\(=(\frac{3}{2})^2+(\sqrt{6})^2\)
\(=\frac{9}{4}+6\)
\(=\frac{9}{4}+\frac{24}{4}\)
\(=\frac{33}{4}\)
donc \((2 ;\sqrt{6}-1)\) appartient à l'ensemble E
Question
c.Quel est la nature géométrique de E, donner ses éléments caractéristiques ?
Solution
\(x_I=\frac{x_A+x_B}{2}=\frac{2-1}{2}=\frac{1}{2}\)
\(y_I=\frac{y_A+y_B}{2}=\frac{-3+1}{2}=-1\)
\(IM^2=\frac{33}{4}\)
M décrit le cercle de centre I milieu de [AB] et de rayon \(\sqrt{\frac{33}{4}}=\frac{\sqrt{33}}{2}\)
la question b. permet de tracer le cercle.
