Exercice : Exercice 39 :
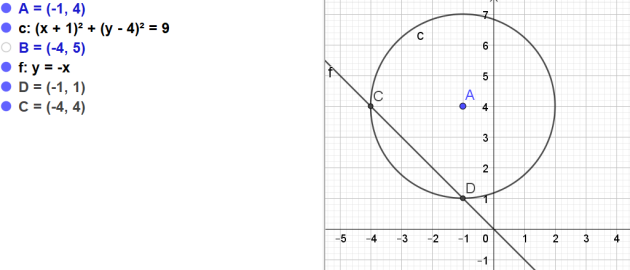
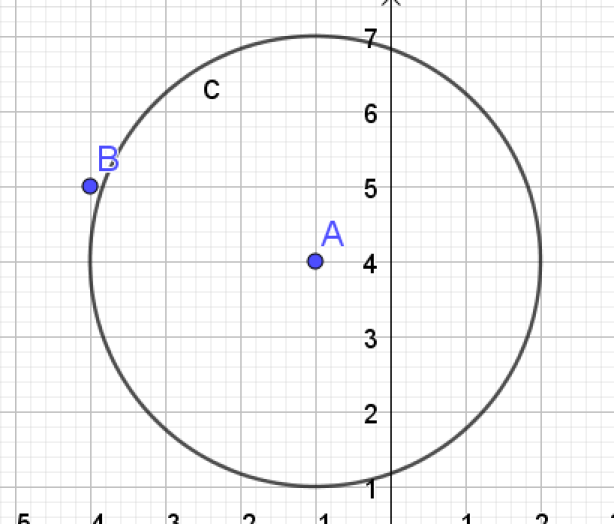
On considère le cercle C de centre A(−1 ; 4) et de rayon 3.
Question
1. Le point B (−4 ; 5) appartient-il au cercle C ?
Solution
\(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}=\sqrt{(-4-(-1))^2+(5-4)^2}\) =\(\sqrt{(-4+1)^2+(1)^2}\)
\(\iff AB=\sqrt{(-3)^2+(1)^2}=\sqrt{9+1}=\sqrt{10}\)
\(\iff \color{red}{AB=\sqrt{10}}\) donc B n'appartient pas au cercle C
Question
2. Expliquer pourquoi un point \(M (x ; y)\) appartient au cercle \(C\) si, et seulement si : \((x + 1)^2 + (y - 4)^2 = 9.\)
Solution
M appartient au cercle C si et seulement si \(AM=3\)
\(\Longleftrightarrow\) \(AM=\sqrt{(x-x_A)^2+(y-y_A)^2}=\sqrt{(x-(-1))^2+(y-4)^2} =\sqrt{(x+1)^2+(y-4)^2} =3\)
\(\Longleftrightarrow\)\(AM^2=(\sqrt{(x+1)^2+(y-4)^2})^2=9\)
\(\Longleftrightarrow\)\(AM^2=(x + 1)^2 + (y - 4)^2=9\)
\(\Longleftrightarrow\color{red}{(x + 1)^2 + (y - 4)^2=9}\)
Question
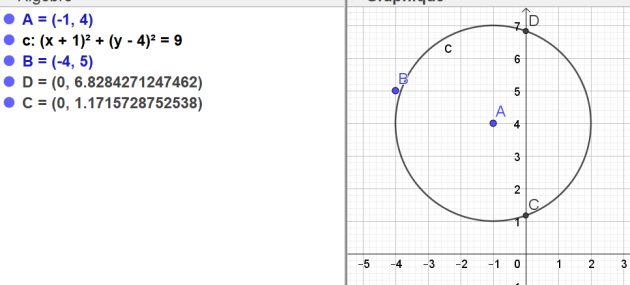
3. Donner une expression exacte des ordonnées des points d'intersection du cercle \(C\) et de la droite d'équation \(x = 0.\)
Solution
\(\begin{cases}x= 0\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\(\iff (0+1)^2+(y-4)^2=9\)
\(\iff 1+(y-4)^2=9\)
\(\iff (y-4)^2=8\)
\(\iff y_1-4=\sqrt{8}\) ou \(y_2-4=-\sqrt{8}\)
\(\iff \color{red}{y_1=4+\sqrt{8}}\simeq6,83\) ou \(\color{red}{y_2=4-\sqrt{8}}\simeq1,17\)
Question
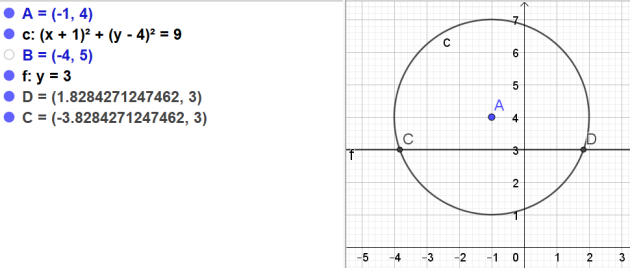
4. Donner une expression exacte des abscisses des points d'intersection du cercle \(C\) et de la droite d'équation y\( = 3\).
Solution
\(\begin{cases}y=3\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\(\iff (x+1)^2+(3-4)^2=9\)
\(\iff (x+1)^2+(-1)^2=9\)
\(\iff x^2+2x+1+1=9\)
\(\iff x^2+2x+2=9\)
\(\iff x^2+2x-7=0\)
\(\Delta=b^2-4ac=2^2-4\times 1 \times (-7)=4+28=32\)
\(\sqrt{\Delta}=\sqrt{32}\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-2-\sqrt{32}}{2}=\frac{-2-\sqrt{16\times 2}}{2}=\frac{-2-4\sqrt{2}}{2}=\color{red}{-1-2\sqrt{2}}\simeq-3 ,83\)\(\mapsto\) \(\color{red}{C(-3 ,83;3)}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-2+\sqrt{32}}{2}==\frac{-2+\sqrt{16\times 2}}{2}=\frac{-2+4\sqrt{2}}{2}=\color{red}{-1+2\sqrt{2}}\simeq1,83\)\(\mapsto\) \(\color{red}{D(1,83 ;3)}\)
Question
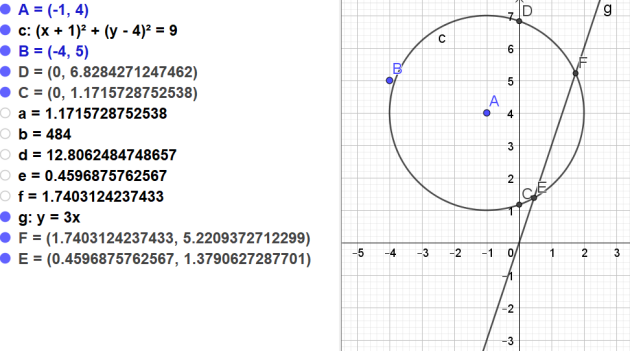
5. Donner une expression exacte des coordonnées des points d'intersection du cercle \(C\) et de la droite d'équation \(y = 3x\).
Solution
\(\begin{cases}y=3x\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\(\iff (x+1)^2+(y-4)^2=9\)
\(\iff (x+1)^2+(3x-4)^2=9\)
\(\iff x^2+2x+1+9x^2-24x+16=9\)
\(\iff 10x^2-22x+17=9\)
\(\iff 10x^2-22x+8=0\)
\(\Delta=b^2-4ac=(-22)^2-4\times 10 \times 8=484-320=164\)
\(\sqrt{\Delta}=\sqrt{164}\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-22)-\sqrt{164}}{2\times 10}\)
\(\iff x_1=\frac{22-\sqrt{4 \times 41}}{20}=\frac{22-2\sqrt{41}}{20}\)
\(\iff \color{red}{x_1=\frac{11-\sqrt{41}}{10}}\simeq0,46\)
\(\mapsto y_1\simeq3 \times 0,46\simeq 1,38\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-22)+\sqrt{164}}{2\times 10}\)
\(\iff x_2=\frac{22+\sqrt{164}}{20}\)
\(\iff x_2=\frac{22+\sqrt{4 \times 41}}{20}=\frac{22+2\sqrt{41}}{20}\)
\(\iff \color{red}{x_2=\frac{11+\sqrt{41}}{10}}\simeq1,74\)
\(\mapsto y_2\simeq3 \times 1,74\simeq 5,22\)
Question
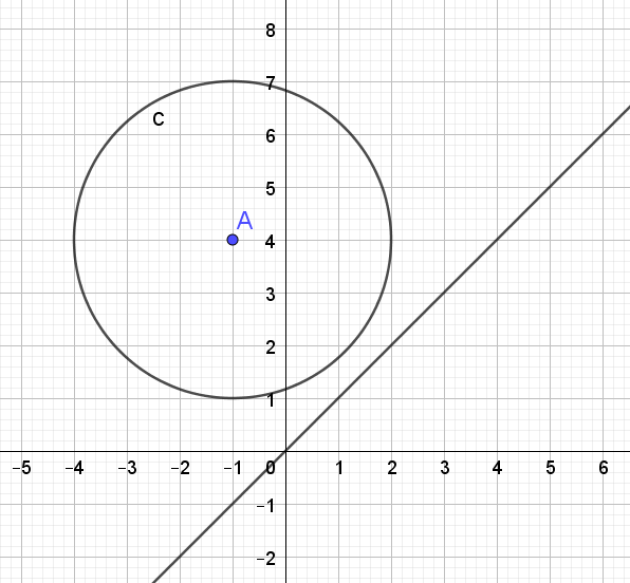
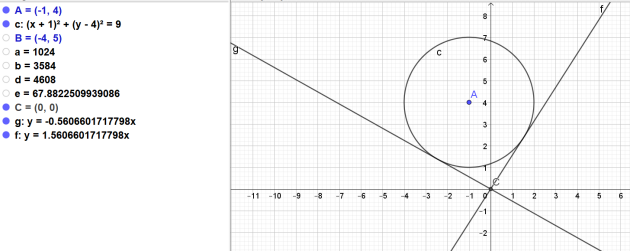
6.On considère un nombre réel m et la droite (d) d'équation\( y = m x.\)
a. Montrer que si m = 1, alors la droite (d) et le cercle \(C\) sont disjoints.
Solution
\(\color{red}{m=1}\)
\(\begin{cases}y=x\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\((x+1)^2+(y-4)^2=9\)
\((x+1)^2+(x-4)^2=9\)
\(x^2+2x+1+x^2-8x+16=9\)
\(2x^2-6x+17=9\)
\(2x^2-6x+8=0\)
\(\Delta=b^2-4ac=(-6)^2-4\times 2 \times 8=36-64=\color{red}{-28}<0\)
donc la droite (d) et le cercle \(C\) sont disjoints.
Question
b.Montrer que si m = −1, alors la droite (d) et le cercle \(C\) ont deux points d'intersection.
Solution
\(\color{red}{m=-1}\)
\(\begin{cases}y=-x\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\((x+1)^2+(y-4)^2=9\)
\((x+1)^2+(-x-4)^2=9\)
\(x^2+2x+1+x^2+8x+16=9\)
\(2x^2+10x+17=9\)
\(2x^2+10x+8=0\)
\(\Delta=b^2-4ac=10^2-4\times 2 \times 8=100-64=36\)
donc la droite (d) et le cercle \(C\) ont deux points communs
\(\sqrt{\Delta}=\sqrt{36}=6\)
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-10-6}{2\times 2}=\frac{-16}{4}=\color{red}{-4}\) \(\mapsto y_1=-1x_1=-1\times (-4)=\color{red}{4}\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-10+6}{2\times 2}=\frac{-4}{4}=\color{red}{-1} \mapsto \)\(y_2=-1x_2=-1\times (-1)=\color{red}{1}\)
Question
7. Calculer les valeurs exactes du paramètre m pour lesquelles pour lesquelles la droite (d) et le cercle C sont tangents.
Solution
\(\begin{cases}y=mx\\ (x + 1)^2+(y-4)^2=9 \end{cases}\)
\((x+1)^2+(y-4)^2=9\)
\((x+1)^2+(mx-4)^2=9\)
\(x^2+2x+1+m^2x^2-8mx+16=9\)
\((m^2+1)x^2+(2-8m)x+17=9\)
\((m^2+1)x^2+(2-8m)x+8=0\)
\(\Delta=b^2-4ac=(2-8m)^2-4\times (m^2+1) \times 8=4-32m+64m^2-32(m^2+1)=64m^2-32m+4-32m^2-32=32m^2-32m-28\)
Si la droite (d) et le cercle \(C\) sont tangents n'ont qu'un seul point commun cela signifie que le discriminant doit être nul donc :
\(32m^2-32m-28=0\)
\(8m^2-8m-7=0\)
\(\Delta=b^2-4ac=(-8)^2-4\times 8 \times (-7)=64+224=284\)
\(\sqrt{\Delta}=\sqrt{284}=\sqrt{4\times 71}=2\sqrt{71}\)
\(m_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-(-8)-2\sqrt{71}}{2\times 8}=\frac{8-2\sqrt{71}}{16}=\color{red}{\frac{4-\sqrt{71}}{8}}\simeq-0,56\)
\(m_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-(-8)+2\sqrt{71}}{2\times 8}=\frac{8+2\sqrt{71}}{16}=\color{red}{\frac{4+\sqrt{71}}{8}}\simeq1,56\)
