Exercice : 3ème ligne de niveau
Deux points A et B sont tels que AB=4
Question
1. Selon la valeur de k, déterminer l'ensemble des points M tels que : \(\vec{MA}.\vec{MB}=k\)
Solution
\(\vec{MA}.\vec{MB}=k\)
\(\iff (\vec{MI}+\vec{IA}).(\vec{MI}+\vec{IB})=k\)
\(\iff \vec{MI}.\vec{MI}+\vec{MI}.\vec{IB}+\vec{IA}.\vec{MI}+\vec{IA}.\vec{IB}=k\)
\(\iff MI^2+\vec{MI}.(\vec{IB}+\vec{IA})+\vec{IA}.\vec{IB}=k\)
or \(\vec{IA}=-\vec{IB}\)
\(MI^2+\vec{MI}.(\vec{IB}-\vec{IB})+(-\vec{IB}).\vec{IB}=k\)
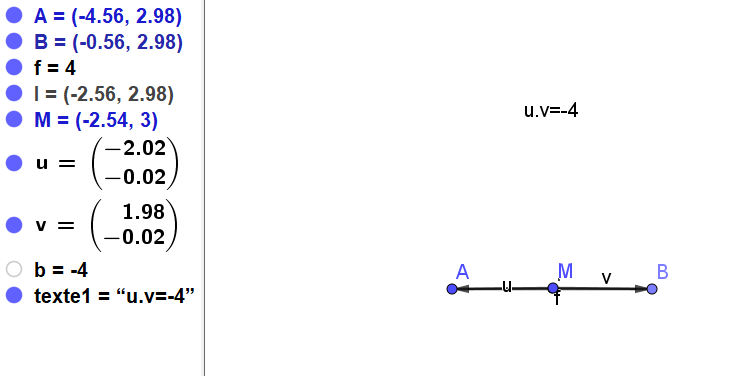
\(\iff MI^2-IB^2=k\)
or IB=2
\(MI^2-4=k\)
\(\iff MI^2=k+4\)
Si \(k>-4\) : le point M décrit le cercle (C) de centre I et de rayon r =\(\sqrt{k+4}\)
Si \(k=-4\) : le point M est le point I (cercle de rayon r=0)
Si \(k<-4\) : le point M n'existe pas (un rayon ne peut être négatif) donc \(S=\emptyset\)
Question
2. C est tel que ABC est un triangle équilatéral.
Comment choisir k pour que C soit un point de \((L_k)\) ?
Solution
\(\vec{CA}.\vec{CB}=||\vec{CA}||\times||\vec{CB}||\times cos(\vec{CA},\vec{CB})\)
\(\iff \vec{CA}.\vec{CB}=4\times4\times cos(\frac{\pi}{3})\)
\(\iff \vec{CA}.\vec{CB}=4\times4\times \frac{1}{2}\)
\(\iff \vec{CA}.\vec{CB}=8\)