Exercice : 1ère ligne de niveau
Dans un repère orthonormé \((O ; \vec{i} ; \vec{j})\) on donne A(-2 ; 2) et B(2 ; 2).
Question
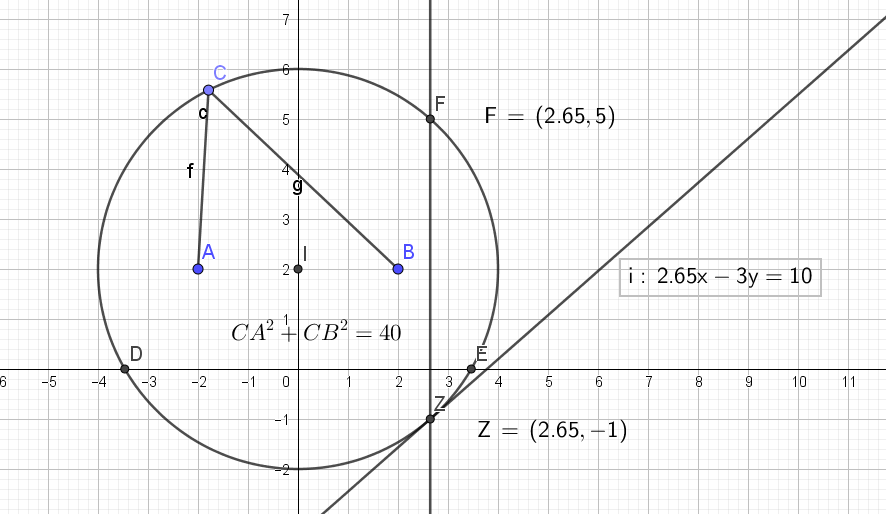
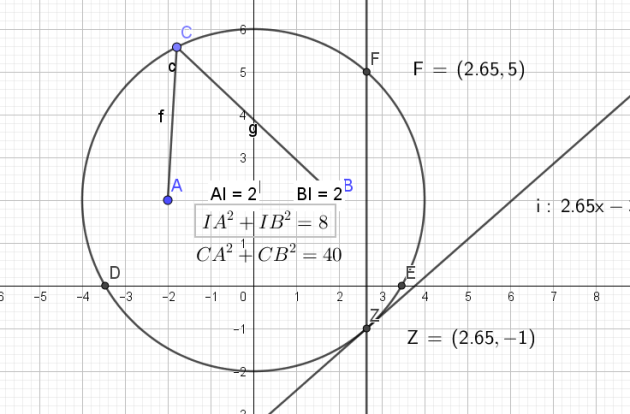
1.Démontrer que l'ensemble des points M du plan tels que \(MA^2 +MB^2 = 40\)
est un cercle (C) de centre I milieu de [AB] et de rayon r = 4.
Solution
\(MA=\sqrt{(x_A-x_M)^2+(y_A-y_M)^2}\)
\(MB=\sqrt{(x_B-x_M)^2+(y_B-y_M)^2}\)
\(MA^2 +MB^2 = 40\)
\(\iff (x_A-x_M)^2+(y_A-y_M)^2+(x_B-x_M)^2+(y_B-y_M)^2=40\)
\(\iff (-2-x_M)^2+(2-y_M)^2+(2-x_M)^2+(2-y_M)^2=40\)
\(\iff (2+x_M)^2+(2-y_M)^2+(2-x_M)^2+(2-y_M)^2=40\)
\(\iff 4+4x_M+x_M^2+4-4y_M+y_M^2+4-4x_M+x_M^2+4-4y_M+y_M^2=40\)
\(\iff 2x_M^2+2y_M^2-8y_M=40-16\)
\(\iff 2x_M^2+2y_M^2-8y_M=24\)
\(\iff x_M^2+y_M^2-4y_M=12\)
\(x_I=\frac{x_A+x_B}{2}=\frac{-2+2}{2}=0\)
\(y_I=\frac{y_A+y_B}{2}=\frac{2+2}{2}=2\)
\(\iff (x_M-0)^2+(y_M-2)^2-4=12\)
\(\iff (x_M-0)^2+(y_M-2)^2=16\)
\(\iff IM^2=16=r^2\)
donc le point M décrit le cercle (C) de centre I et de rayon r = 4.
Question
2.Déterminer les coordonnées des éventuels points d'intersection de (C) avec l'axe des abscisses.
Solution
\((x_M-0)^2+(y_M-2)^2=16\)
Soit \(x_M\) l'abscisse d'un point d'intersection du cercle (C) et de l'axe des abscisses.
Si le point appartient à l'axe des abscicces, c'est que son ordonnée \(y\) est nulle.
\((x-0)^2+(0-2)^2=16\)
\(\iff x^2+4=16\)
\(\iff x^2=12\)
\(\iff x^2=12\)
\(\iff x=\sqrt{12}=\sqrt{4 \times 3}=2\sqrt{3}\) ou \(x=-\sqrt{12}=-\sqrt{4 \times 3}=-2\sqrt{3}\)
Question
3.Soit α un réel négatif. Comment choisir α pour que le point Z(\(\sqrt{7}\) ; α) soit sur (C).
Solution
\((\sqrt{7}-0)^2+(\alpha-2)^2=16\)
\(\iff \sqrt{7}^2+(\alpha-2)^2=16\)
\(\iff 7+(\alpha-2)^2=16\)
\(\iff 7+(\alpha-2)^2=16\)
\(\iff (\alpha-2)^2=9\)
\(\iff \alpha-2=3\) ou \(\alpha-2=-3\)
\(\iff \alpha=5\) ou \(\alpha=-1\)
Comme \(\alpha<0\) le point Z est le point de coordonnées \((\sqrt{7} ;-1)\)
Question
4.Déterminer une équation de la tangente (T) à (C) au point Z.
Solution
Soit N un point de la tangente au cercle au point Z :
\(\vec{IZ}.\vec{ZN}=0\)
\(\iff \left( \begin{array}{c}\sqrt{7}-0\\-1-2\end{array} \right) . \left( \begin{array}{c}x-\sqrt{7}\\y-(-1)\end{array} \right)=0\)
\(\iff \left( \begin{array}{c}\sqrt{7}\\-3\end{array} \right) . \left( \begin{array}{c}x-\sqrt{7}\\y+1\end{array}\right)=0\)
\(\iff \sqrt{7}(x-\sqrt{7})-3(y+1)=0\)
\(\iff \sqrt{7}x-7-3y-3=0\)
\(\iff \sqrt{7}x-3y-10=0\)
Question
5.Donner suivant la valeur du réel k, l'ensemble des points M tels que \(MA^2+ MB^2=k\)
Solution
\(MA=\sqrt{(x_A-x_M)^2+(y_A-y_M)^2}\)
\(MB=\sqrt{(x_B-x_M)^2+(y_B-y_M)^2}\)
\(MA^2 +MB^2 = k\)
\(\iff (x_A-x_M)^2+(y_A-y_M)^2+(x_B-x_M)^2+(y_B-y_M)^2=k\)
\(\iff (-2-x_M)^2+(2-y_M)^2+(2-x_M)^2+(2-y_M)^2=k\)
\(\iff (2+x_M)^2+(2-y_M)^2+(2-x_M)^2+(2-y_M)^2=k\)
\(\iff 4+4x_M+x_M^2+4-4y_M+y_M^2+4-4x_M+x_M^2+4-4y_M+y_M^2=k\)
\(\iff 2x_M^2+2y_M^2-8y_M=k-16\)
\(\iff x_M^2+y_M^2-4y_M=\frac{k-16}{2}\)
\(\iff (x_M-0)^2+(y_M-2)^2=\frac{k-16}{2}\)
\(\iff (x_M-0)^2+(y_M-2)^2=\frac{k-16}{2}+4\)
\(\iff (x_M-0)^2+(y_M-2)^2=\frac{k-16}{2}+\frac{8}{2}\)
\(\iff (x_M-0)^2+(y_M-2)^2=\frac{k-8}{2}\)
Si k>8 : le point M décrit le cercle (C) de centre I et de rayon \(r =\sqrt{\frac{k-8}{2}}=\frac{\sqrt{k-8}}{\sqrt{2}}=\frac{\sqrt{2}\sqrt{k-8}}{2}\)
Si k=8 : le point M est le point I (cercle de rayon r=0)
Si k<8 : le point M n'existe pas (un rayon ne peut être négatif) donc \(S=\emptyset\)
